Yet Another Training Metric 1
This experiment is lifted from a project I did with Ivan Lee for APMA2822b.
In the past couple of years, Phillipe Rigollet’s group at MIT has been putting out theoretical work on a dynamical model for transformers 1. Instead of studying the training dynamics of transformers, they study the forward pass dynamics of transformers i.e. how the token distribution changes after each transformer block.
Because modern transformers employ skip connections and normalization, the forward propagation of a transformer can been viewed as a series of normalized additive updates to a running state:
\[x_{t+1} = \text{N}(x_t + \text{Module}(x_t; \theta_t))\]where $x_t$ is the state, $\text{N}$ is some normalization function (e.g. LayerNorm), and $\theta_t$ parameterizes the module (e.g. for attention it would be the QKVO matrices). This idea also underlies the “residual stream”, a fundamental framework in modern interpretability.
Naturally, we can then consider the continuous time / infinite depth limit (see “neural ODEs”) of this system
\[\dot{x} = \mathbf{P}_{x_t}^\perp(\text{Module}(x_t; \theta_t))\]where $\mathbf{P}^\perp_{x_t}$ is just notation for a projection operator that projects $\text{Module}(x_t;\theta_t)$ onto the tangent space of the normalized manifold at $x_t$ (e.g. if $\text{N}$ makes everything unit norm, then the “normalized manifold” would be the sphere).
The key takeaway is we can treat the transformer forward pass as the path of a set of particles through the normalized manifold. In this case, $x_0$ is the $n \times d$ sequence of token embeddings, $\text{Module}$ is the single-head attention operation (with/without causal masking), and $\text{N}$ scales vectors to unit norm. The main simplifications from empirical transformers made for the sake of theoretical analysis are omitting MLPs, single-head attention, and unit normalization instead of LayerNorm.
In this model, under suitable (and imo extremely restrictive) assumptions on $\theta_t$, there exists a monotonically increasing quantity along the flow, namely the interaction energy 2
\[\frac{1}{n^2}\sum_{i=1}^n \sum_{j=1}^n e^\frac{\langle x_i, x_j\rangle}{\|x_i\|_2 \|x_j\|_2}.\]As intuition, the interaction energy is maximized when $x$ is $n$ vectors in the same direction and minimized when $x$ is directionally uniform - almost like an inverse entropy. High interaction energy indicates clustering of predictions to some direction in embedding space, whereas low interaction energy indicates “spread out” predictions.
Interaction Energy Over Training
Here, we look at how interaction energy changes over training time and what it can tell us about how the model trained. For a few different Pythia models, we plot two quantities over training time: (1) the interaction energy at the final layer (blue) and (2) the KL divergence of output predictions to the unigram token distribution (orange), both averaged over a subset of samples from openwebtext-10k.
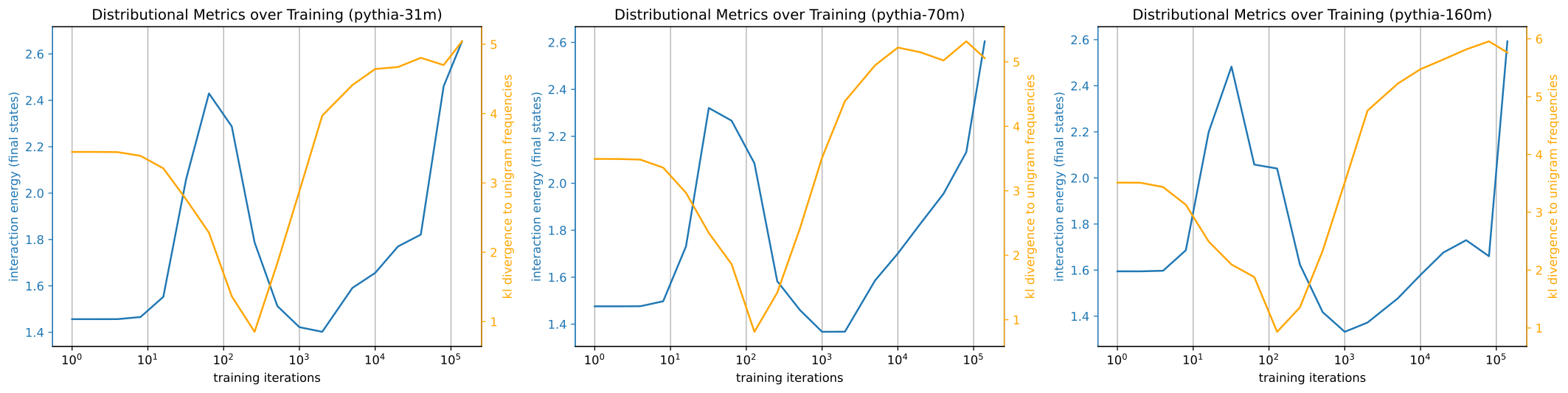
These two metrics in tandem tell a story about how this model developed. Indeed, the critical points of the metric curves split training into phases:
- Model quickly learns to predict the unigram distribution (KL low) consistently across tokens (IE high).
- Model begins moving away from predicting just the unigram distribution at each token (KL increasing, IE decreasing).
- Model converging to similar predictions again (IE up), but it is no longer the unigram distribution (KL still high).
Pretty neat! The models quickly pick up on the unigram distribution, the simplest statistic, and predicts distributions close to it before switching to learning higher order relationships in a sort of “stagewise” development.
These results are also connected to the GPT2 is unigram-ist post I made last year, where I looked at the trainability of a latent $x$ that induces the unigram distribution when unembedded over training time. I found that, very early on in training, models establish a direction that unembeds to a distribution close to the unigram distribution, corroborating what we found here.
The interaction energy just fills in the story more: soon after establishing this direction, the model begins relatively consistently (indicated by interaction energy) leveraging that latent direction to output predictions similar to the unigram distribution (indicated by KL divergence to unigram distribution).
Brief Commentary on this Body of Work
Now, as for other applications of this quantity - I’m not too sure. The main quirk is that interaction energy is estimated in embedding space (unlike entropy) and seems to capture the notion of the attention converging to a prediction through the forward pass. Studying in embedding space rather than logit space likely better captures internal computations that do not appear in the logits. But it’s not obvious whether interaction energy should be high or low - it just tells you something about what’s being predicted.
This dynamics model has been fruitful theoretically: many connections are made to celebrated models in statistical physics and results like metastable clustering for exponential time 3 are unique. But, IMO, it falls short in offering impactful empirical insight. Their main results (e.g. clustering, monotonic quantities) are all obtained under questionably strong assumptions (time independence of parameters, identity value matrix, etc.) that weaken the results greatly, and confronting them is much of what people believe to make transformers tick. For example, nontrivial attention head composition can only exist in time dependent parameters.
-
The original paper does not scale by the norms of $x_i$ and $x_j$ because both are always on the unit sphere (due to $\text{N}$). We will compute this quantity on actual autoregressive transformers, so we need to normalize somehow to avoid numerical blowup. It’s a weird generalization that I’m unsatisfied with because norms of internal states matters (e.g. it affects the entropy of logits after decoding). ↩